Optimized estimation and bias-aware inference for treatment effects identified by regression discontinuities under partially linear model as proposed by Ghosh, Imbens and Wager (2025).
Usage
plrd(
Y,
X,
threshold,
W = NULL,
max.window = NULL,
Lipschitz.constant = NULL,
sigma.sq = NULL,
alpha = 0.95,
diff.curvatures = FALSE,
signif.curvature = 0.001,
bin.width = NULL,
num.bucket = 400,
use.spline = TRUE,
spline.df = 40,
seed = 42,
use.homoskedastic.variance = FALSE,
verbose = FALSE
)Arguments
- Y
The outcomes.
- X
The running variable.
- threshold
Sharp Regression Discontinuity threshold "c" at which CATE is to be estimated.
- W
The treatment indicator. Currently plrd only supports sharp RDD, hence W is set as NULL by default.
- max.window
A reasonable window for estimating the Lipschitz bound on curvature accurately. Default is the whole range.
- Lipschitz.constant
A Lipschitz bound for the second derivative of mu_w(x) = E(Y(w) | X = x).
- sigma.sq
An estimate of the homoskedastic variance of Y conditional on X
- alpha
Coverage probability of confidence intervals.
- diff.curvatures
Set true if user believes the curvatures are different before and after the threshold c.
- signif.curvature
Significance level for testing whether curvature is different before and after the threshold.
- bin.width
Bin width for discrete approximation.
- num.bucket
Number of bins for discrete approximation. Can only be used if bin.width = NULL.
- use.spline
Whether non-parametric components should be modeled as cubic splines in order to reduce the number of optimization parameters, and potentially improving computational performance.
- spline.df
Number of degrees of freedom (per running variable) used for spline computation.
- seed
Random seed for reproducibility.
- use.homoskedastic.variance
Whether confidence intervals should be built assuming homoskedasticity. As default we use FALSE (i.e., use heteroscedastic standard errors).
- verbose
Whether the optimizer should print progress information.
Value
A trained plrd object containing the PLRD estimator, half width of confidence interval and other auxiliary objects such as MSE-optimal weights, worst-case bias, Lipschitz constant, etc.
References
Ghosh, A., Imbens, G., & Wager, S. (2025). PLRD: Partially Linear Regression Discontinuity Inference. arXiv preprint arXiv:2503.09907.
Examples
# \donttest{
# Simple example of regression discontinuity design
set.seed(42)
n = 1000; threshold = 0
X = runif(n, -1, 1)
W = as.numeric(X >= threshold)
Y = (1 + 2*W)*(1 + X^2) + 1 / (1 + exp(X)) + rnorm(n, sd = .5)
out = plrd(Y, X, threshold)
print(out)
#> Partially linear regression discontinuity inference:
#> Threshold: 0
#> Lipschitz constant: 7.302
#> Max bias: 0.05186
#> Sampling SE: 0.0856
#> Confidence level: 95%
#>
#> Estimate CI Lower CI Upper p-value
#> RD Estimate 2.022 1.828 2.217 1.461e-117
plot(out)
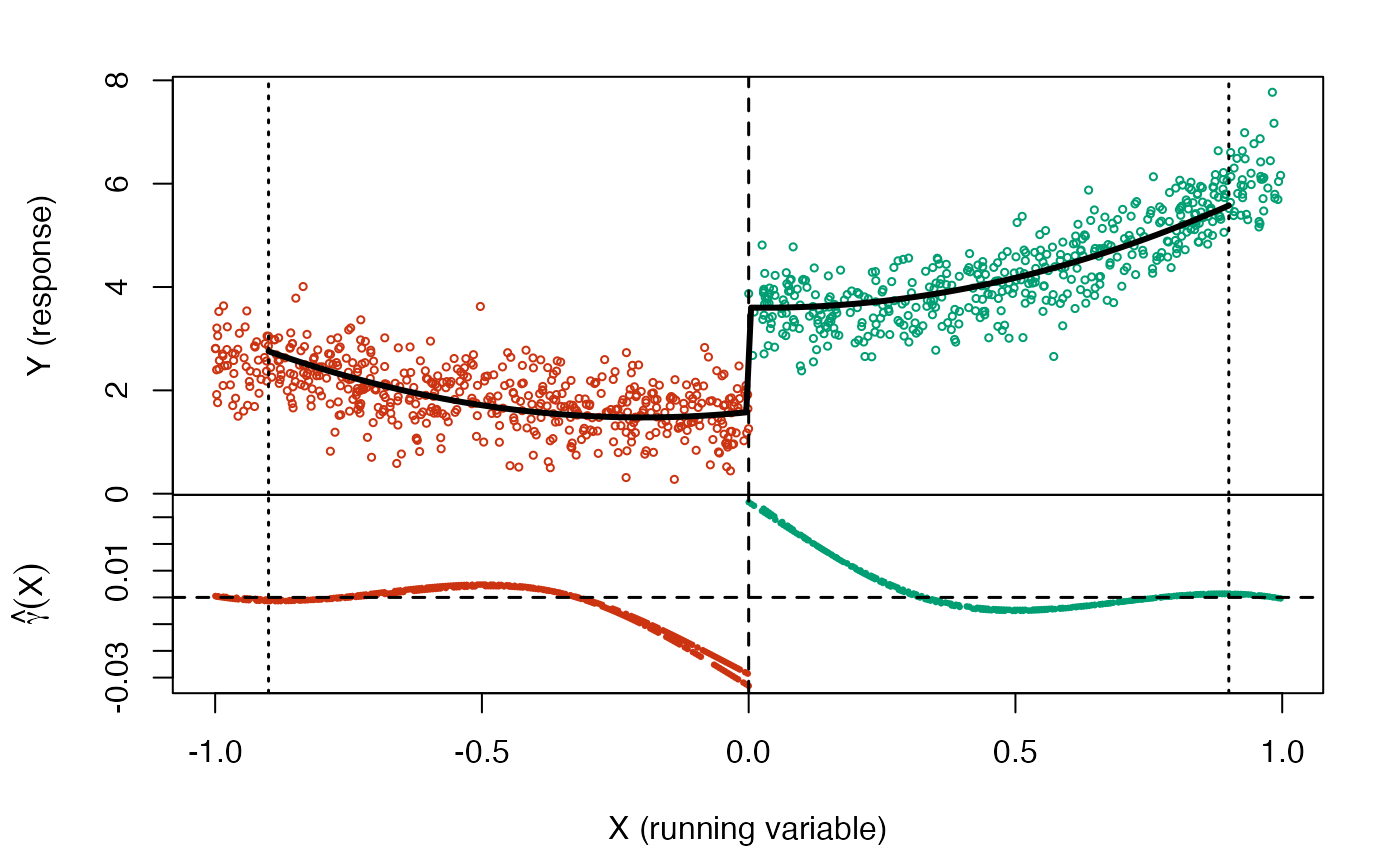#> [1] "The black curves in the top panel are representative regression functions in our data-driven function class. The dashed line shows the threshold, and the dotted lines indicate the window containing 95% of the cumulative absolute weights. The bottom panel shows two sets of plrd weights because we use cross-fitting."
# }